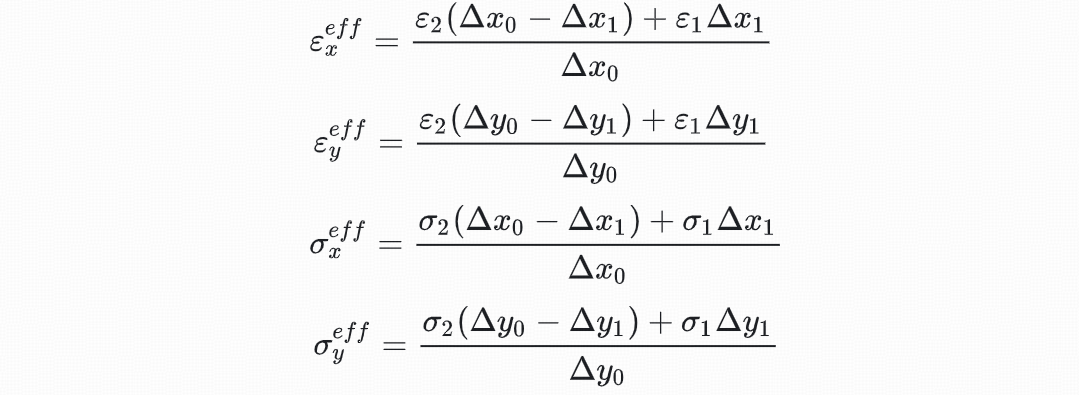1. 前言
在FDTD方法当中,时间空间等均由Yee网格表示,这种离散方法也会带来一些系统性误差,例如网格色散等。此外,通过离散差分所能模拟的最小尺度即为一个网格,对于小于一个网格尺寸的结构,只能近似为一个网格,这将会给数值计算带来误差。当然最简单有效的办法是将网格划分得足够细,但这将需要更多的计算资源和时间。另一种方法则是使用共形网格,这种方法可以让整个计算区域的网格保持较大尺寸,同时,修正局部网格来减小误差。
2. 网格色散
首先我们需要了解在FDTD网格离散化时所带来的数值不稳定性。由于空间和时间均由离散化的网格表示,时间空间离散间隔的选取将决定差分方程的解是否是收敛和稳定的。
考虑平面波的解,即 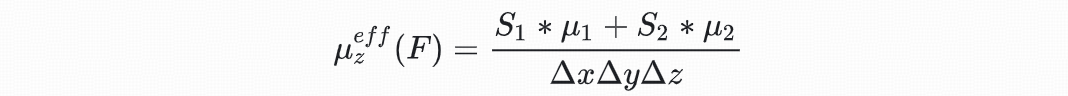 ,其二阶导进行差分近似可以得到
,其二阶导进行差分近似可以得到
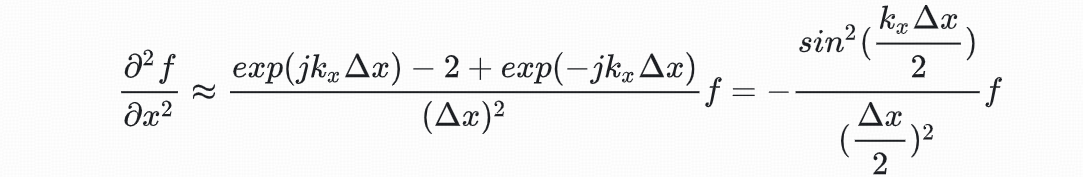
将该离散差分的结果代入波动方程可以得到色散关系式

再将时间离散化,得到的不等式如下

该式即为Courant稳定性条件。对于三维情况下的立方体元胞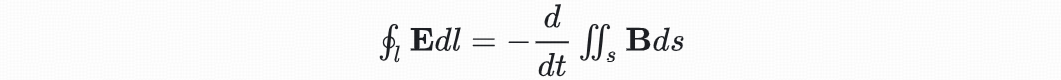 有:
有:
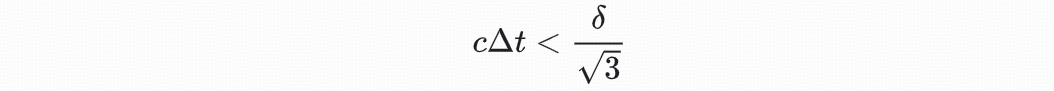
当为二维正方形网格 时为
时为

以上两种情况下,说明时间间隔须小于波以光速通过元胞对角线长度1/3(三维)或1/2(二维)所需的时间。 上述的色散关系式可以看出:即使计算当中并没有色散材料以及损耗材料,由于离散差分近似,波矢k与频率ω之间已经不是简单的线性关系式,必然导致相速度与频率有关,从而出现色散。将色散关系式简化到一维情况下

计算相速度为
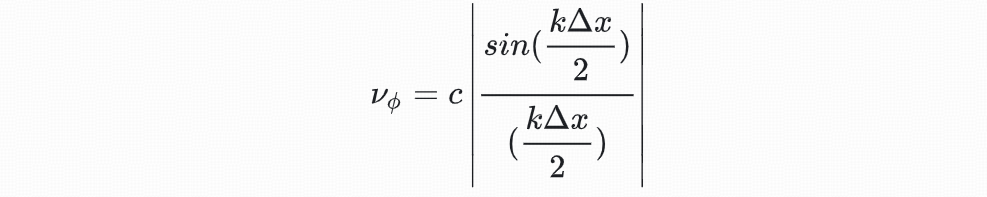
而当角度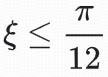 时,可以认为
时,可以认为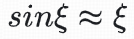 ,即得到空间离散间隔的满足条件
,即得到空间离散间隔的满足条件
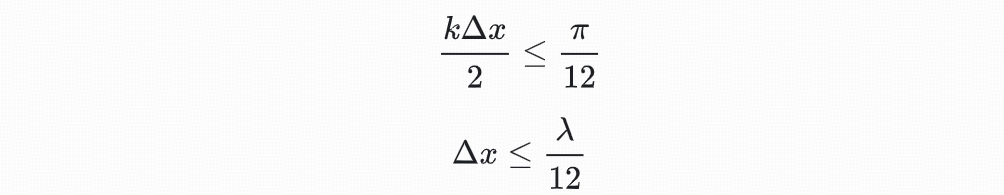
同理可得时间离散间隔
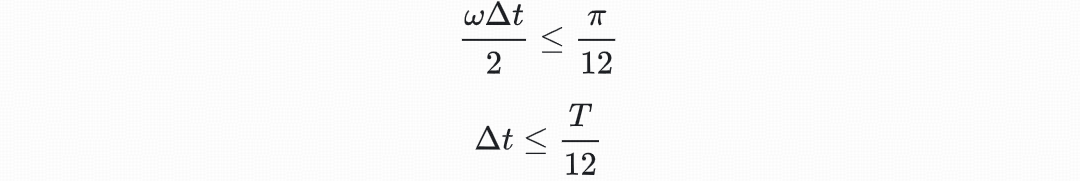
在实际计算当中,采用何种时间空间离散间隔还需要视需求而定。
3. 网格细化
3.1 均匀网格
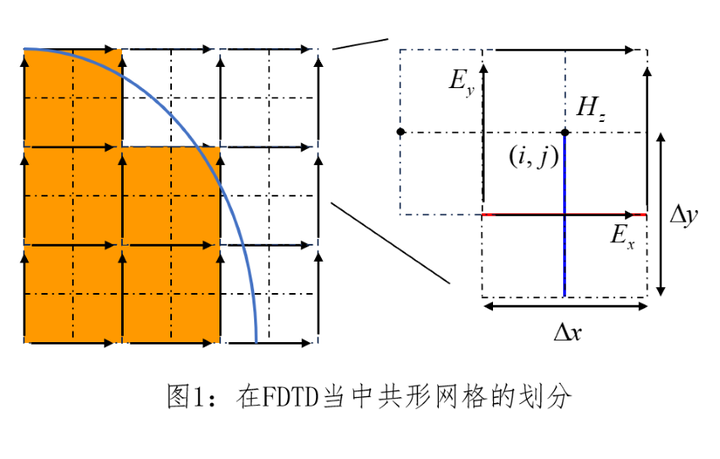
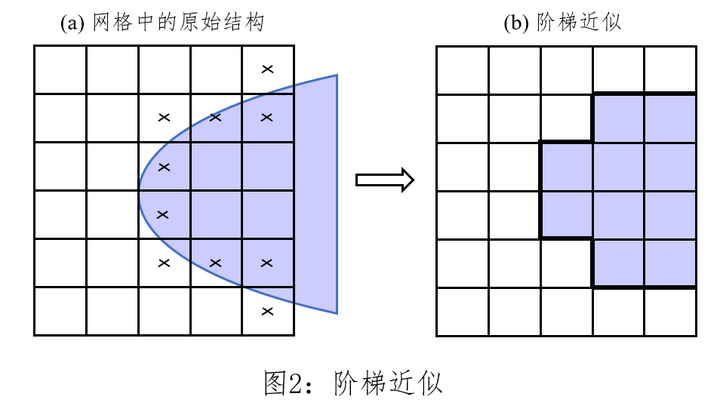
在均匀网格中,对于小于网格尺寸的结构一般使用网格中心点判断该网格处的材料参数,该处理方式称为阶梯近似,如下图所示。
3.2 非均匀网格
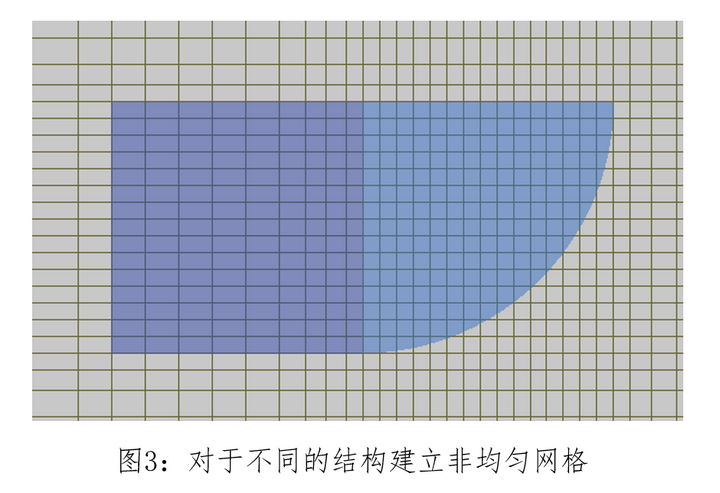
而非均匀网格可以根据需求以及物理场的变化情况来对应调整网格单元的尺寸,因此使用非均匀网格可以更好地捕捉物理场的细节和变化,同时对于折射率变化不明显的地方使用较大的网格尺寸也可以提高计算效率。非均匀网格是FDTD方法当中一种重要技术,可以提高模拟的准确性和效率,能够更好地适应不同的物理模型。 如下图,对于结构复杂的弧形结构,自动根据材料和形状建立更密的网格来获得其边界的细节,而对于规则的矩形将建立相对尺寸较大的网格。这种方式可以在不损失材料精确度的情况下尽量节省计算资源。
3.3 共形网格
共形网格通过在网格细化方法上做出优化,能够得到Yee单元结构内的等效材料分布。在FDTD计算中,共形网格技术可以处理曲线边界、不规则形状等复杂情况,可以实现对复杂几何形状的精确建模和模拟,提高了模拟结果的准确性和计算效率。目前共形网格技术已经发展出多套理论和方法,对于该技术,在此简单地介绍两种以作了解。
3.4 介质体平均
介质体平均是共形网格技术当中基本的方法之一,其在网格当中以各种介质所占据的体积来计算该网格的等效材料常数。这种方法没有太多物理意义,操作简单,对折射率对比度低的介质表面有效。下图展示了这种方法示意图,图中认为结构在z方向分布相同,因此仅绘出二维截面。
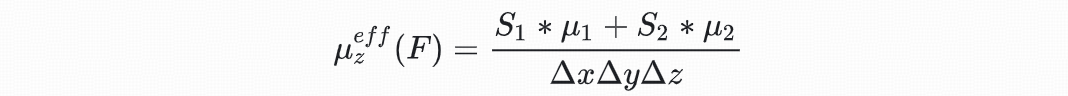
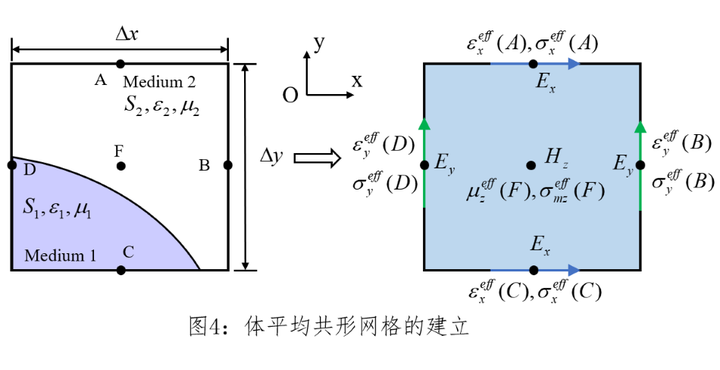
其中,S1,S2为介质1,介质2所占的体积。由上述介绍可知,介质体平均的方法在描述复杂结构的电磁特性时存在一定的局限性。这种方法通常假设介质体在空间上是均匀分布的,而忽略了结构内部分布的不均匀性。因此不同结构在网格单元内的实际分布可能会有很大的差异,但通过介质体平均得到的等效材料参数却可能相同。这正是介质体平均方法的局限性。
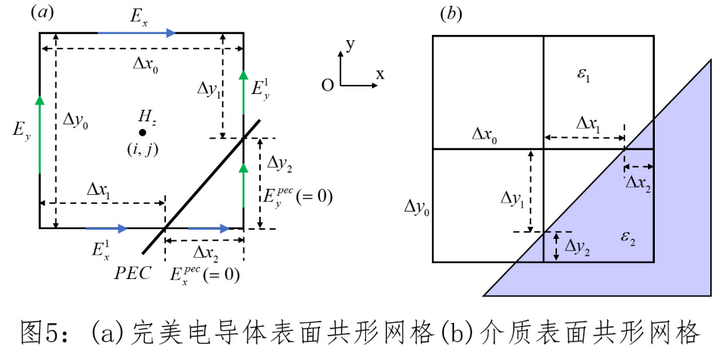
3.5 Yu-Mittra共形网格方法
Yu-Mittra共形网格方法由Yu和Mittra于2001年提出,利用了如图中所示的线性平均概念和电场在材料界面的特性,从而实现了对复杂边界的精确建模和模拟。现如今已经成为FDTD当中一种常见方法,基于该方法,已经有多种改进方法应用在FDTD中。原始的Yu-Mittra共形网格方法是为了解决理想导体与介电材料界面处的精度计算。理想导体内部电场为零,故有法拉第电磁感应定律
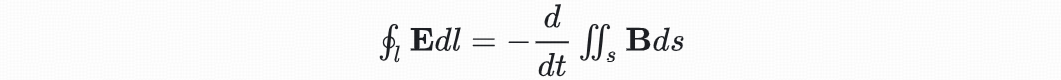
可以得到二维FDTD迭代方程
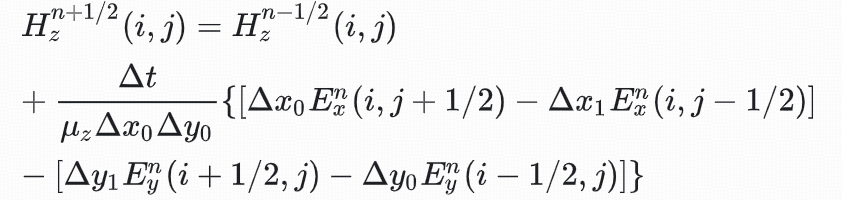
进一步的可以将其应用到介质表面的共形网格当中。